The sinus hyperbolicus function

Up a level : The hyperbolic functions
Previous page : Hyperbolic functions – The cosinus hyperbolicus and its inverse

So if

x = \frac{{{e^\theta } + {e^{ - \theta }}}}{2} = \cosh \theta  

and

y = \sqrt {{x^2} - 1}  

then

\begin{gathered}   y = \;\sqrt {{{\left( {\frac{{{e^\theta } + {e^{ - \theta }}}}{2}} \right)}^2} - 1}  \hfill \\   \quad  = \sqrt {\frac{{{e^{2\theta }} + 2 + {e^{ - 2\theta }}}}{4} - 1}  \hfill \\   \quad  = \sqrt {\frac{{{e^{2\theta }} + 2 + {e^{ - 2\theta }}}}{4} - \frac{4}{4}}  \hfill \\   \quad  = \sqrt {\frac{{{e^{2\theta }} - 2 + {e^{ - 2\theta }}}}{4}}  \hfill \\   \quad  = \sqrt {{{\left( {\frac{{{e^\theta } - {e^{ - \theta }}}}{2}} \right)}^2}}  \hfill \\   \quad  = \frac{{{e^\theta } - {e^{ - \theta }}}}{2} = \sinh \theta  \hfill \\  \end{gathered}  

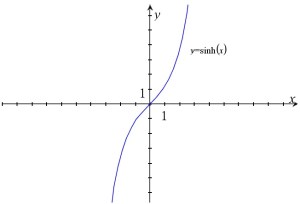
The graph of this is seen below.

We can compare this with the exponential form of the sine function found here.

sin(\theta ) = \frac{{{e^{i\theta }} - {e^{ - i\theta }}}}{{2i}}

The inverse function

We get

\begin{gathered}   y = \;\frac{{{e^\theta } - {e^{ - \theta }}}}{2} = \sinh \theta \quad \quad // \cdot 2 \hfill \\   2y = \;{e^\theta } - {e^{ - \theta }}\quad \quad \quad \quad \quad //w = {e^\theta } \hfill \\   2y = \;w - \frac{1}{w}\quad \quad \quad \quad \quad \quad // \cdot w \hfill \\   2yw = \;{w^2} - 1\quad \quad \;\;\quad \quad \quad // - 2yw \hfill \\   0 = \;{w^2} - 2yw - 1 \hfill \\  \end{gathered}  

The quadratic formula now gives us (with a=1, b= –2y and c= –1).

\begin{gathered}   w = \frac{{ - ( - 2y) \pm \sqrt {4{y^2} - 4 \cdot 1 \cdot ( - 1)} }}{{2 \cdot 1}} \hfill \\   \quad  = \frac{{2y \pm \sqrt 4 \sqrt {{y^2} + 1} }}{{2 \cdot 1}} \hfill \\   \quad  = y \pm \sqrt {{y^2} + 1}  \hfill \\ \end{gathered}  

This gives us

y = \ln \left( {y \pm \sqrt {{y^2} + 1} } \right)

So what sign to use?  If we use the negative sign we get the log of a negative number, so we must have

y = \ln \left( {y + \sqrt {{y^2} + 1} } \right) = {\sinh ^{ - 1}}y

The graph of this can be seen below.

Up a level : The hyperbolic functions
Previous page : Hyperbolic functions – The cosinus hyperbolicus and its inverseLast modified: May 21, 2019 @ 20:04